DEFINICIÓN DE
PROPORCIÓN ÁUREA
La proporción áurea es un número irracional que descubrieron pensadores de la Antigüedad al advertir el vínculo existente entre dos segmentos pertenecientes a una misma recta. Dicha proporción puede hallarse en la naturaleza (flores, hojas, etc.) y en figuras geométricas y se le otorga una condición estética: aquello cuyas formas respetan la proporción áurea es considerado bello.
Esta proporción, que también suele mencionarse como razón áurea, número áureo o divina proporción, incluso solía ser señalada por sus supuestas propiedades místicas. Su ecuación se expresa como 1 más la raíz cuadrada de 5, todo sobre 2, y el resultado es aproximadamente igual a 1,61803398874989…
El rectángulo áureo de Euclides
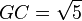 El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo. Euclides, en su proposición 2.11 de Los elementos, obtiene su construcción:
El rectángulo AEFD es áureo porque sus lados AE y AD están en la proporción del número áureo. Euclides, en su proposición 2.11 de Los elementos, obtiene su construcción:
Con centro en G se obtiene el punto E, y por lo tanto:
con lo que resulta evidente que
de donde, finalmente,

Fibonacci
Si se denota el enésimo número de Fibonacci como Fn, y al siguiente número de Fibonacci como Fn + 1, descubrimos que, a medida que n aumenta, esta razón oscila y es alternativamente menor y mayor que la razón áurea. Podemos también notar que la fracción continua que describe al número áureo produce siempre números de Fibonacci a medida que aumenta el número de unos en la fracción. Por ejemplo: ;
;  ; y
; y  , lo que se acerca considerablemente al número áureo. Entonces se tiene que:Esta propiedad fue descubierta por el astrónomo alemán Johannes Kepler, pero pasaron más de cien años antes de que fuera demostrada por el matemático inglés Robert Simson.Con posterioridad se encontró que cualquier sucesión aditiva recurrente de orden 2 tiende al mismo límite. Por ejemplo, si tomamos dos números naturales arbitrarios, por ejemplo 3 y 7, la sucesión recurrente resulta: 3 - 7 - 10 - 17 - 27 - 44 - 71 - 115 - 186 - 301... Los cocientes de términos sucesivos producen aproximaciones racionales que se acercanasintóticamente por exceso y por defecto al mismo límite: 44/27 = 1,6296296...; 71/44 = 1,613636...; 301/186 = 1,6182795.11A mediados del siglo XIX, el matemático francés Jacques Philippe Marie Binet redescubrió una fórmula que aparentemente ya era conocida por Leonhard Euler, y por otro matemático francés, Abraham de Moivre. La fórmula permite encontrar el enésimo número de Fibonacci sin la necesidad de producir todos los números anteriores. La fórmula de Binet depende exclusivamente del número áureo:
, lo que se acerca considerablemente al número áureo. Entonces se tiene que:Esta propiedad fue descubierta por el astrónomo alemán Johannes Kepler, pero pasaron más de cien años antes de que fuera demostrada por el matemático inglés Robert Simson.Con posterioridad se encontró que cualquier sucesión aditiva recurrente de orden 2 tiende al mismo límite. Por ejemplo, si tomamos dos números naturales arbitrarios, por ejemplo 3 y 7, la sucesión recurrente resulta: 3 - 7 - 10 - 17 - 27 - 44 - 71 - 115 - 186 - 301... Los cocientes de términos sucesivos producen aproximaciones racionales que se acercanasintóticamente por exceso y por defecto al mismo límite: 44/27 = 1,6296296...; 71/44 = 1,613636...; 301/186 = 1,6182795.11A mediados del siglo XIX, el matemático francés Jacques Philippe Marie Binet redescubrió una fórmula que aparentemente ya era conocida por Leonhard Euler, y por otro matemático francés, Abraham de Moivre. La fórmula permite encontrar el enésimo número de Fibonacci sin la necesidad de producir todos los números anteriores. La fórmula de Binet depende exclusivamente del número áureo:

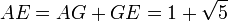

![F_n = \frac{1}{\sqrt{5}} \left [ \left (\frac{1 +\sqrt{5}}{2} \right )^n - \left (\frac{1 - \sqrt{5}}{2}\right )^n \right ]\quad=\frac{1}{\sqrt{5}} \left [ \left ( \phi \right )^n - \left (\frac{-1}{\phi} \right )^n \right ] \quad](https://upload.wikimedia.org/math/e/5/a/e5ab287a1c0dfbf356434045bce90d0c.png)
No hay comentarios:
Publicar un comentario